Separate Source Channel Coding Is Still What You Need: An LLM-Based Rethinking

doi:10.12142/ZTECOM.202501005

ZTE Communications ›› 2025, Vol. 23 ›› Issue (1): 30-44.DOI: 10.12142/ZTECOM.202501005

• Special Topic • Previous Articles Next Articles

Separate Source Channel Coding Is Still What You Need: An LLM-Based Rethinking

REN Tianqi¹, LI Rongpeng¹(), ZHAO Mingmin¹, CHEN Xianfu², LIU Guangyi³, YANG Yang⁴, ZHAO Zhifeng¹^,⁵, ZHANG Honggang⁶

^1.College of Information Science and Electronic Engineering, Zhejiang University, Hangzhou 310027, China
^2.Shenzhen CyberAray Network Technology Co. , Ltd. , Shenzhen 518000, China
^3.China Mobile Research Institute, Beijing 100053, China
^4.The Internet of Things Thrust, The Hong Kong University of Science and Technology (Guangzhou), Guangzhou 511453, China
^5.Zhejiang Lab, Hangzhou 311121, China
^6.Faculty of Data Science, City University of Macau, Macao 999078, China

Received:2025-01-02 Online:2025-03-25 Published:2025-03-25
About author:REN Tianqi received his BE degree in electronic science and technology from Zhejiang University, China in 2024. He is currently pursuing his ME degree in electronic and information engineering with Zhejiang University. His research interests include application of large language models in communication scenarios and semantic communications.
LI Rongpeng (lirongpeng@zju.edu.cn) is currently an associate professor with the College of Information Science and Electronic Engineering, Zhejiang University, China. He was a research engineer with the Wireless Communication Laboratory, Huawei Technologies Co., Ltd. from August 2015 to September 2016. He was a visiting scholar with the Department of Computer Science and Technology, University of Cambridge, UK from February 2020 to August 2020. His research interest currently focuses on networked intelligence for communications evolving (NICE). He received the Wu Wenjun Artificial Intelligence Excellent Youth Award in 2021. He serves as an Editor for China Communications.
ZHAO Mingmin received his BEng and PhD degrees in information and communication engineering from Zhejiang University, China in 2012 and 2017, respectively. From December 2015 to August 2016, he was a visiting scholar with the Department of Electrical and Computer Engineering, Iowa State University, USA. From July 2017 to July 2018, he was a research engineer with Huawei Technologies Co., Ltd. He is currently a lecturer with the College of Information Science and Electronic Engineering, Zhejiang University. Since May 2019, he has been a visiting scholar with the Department of Electrical and Computer Engineering, National University of Singapore. His research interests include channel coding, algorithm design and analysis for advanced MIMO, cooperative communication, and machine learning for wireless communications.
CHEN Xianfu received his PhD degree (with Hons.) from Zhejiang University, China in 2012. In 2012, he joined the VTT Technical Research Centre of Finland, as a research scientist and as a senior scientist from 2013 to 2023. He is currently a chief research engineer with the Shenzhen CyberAray Network Technology Co., Ltd., China. His research interests include various aspects of wireless communications and networking, with emphasis on human-level and artificial intelligence for resource awareness in next-generation communication networks. Dr. CHEN was the recipient of the 2021 IEEE Communications Society Outstanding Paper Award and the 2021 IEEE Internet of Things Journal Best Paper Award. He is an editor of IEEE Open Journal of the Communications Society, an academic editor of Wireless Communications and Mobile Computing, and an associate editor of China Communications.
LIU Guangyi received his PhD degree from Beijing University of Posts and Telecommunications, China in 2006. He is currently the chief scientist of 6G in China Mobile Communication Corporation (CMCC), the founding member and the co-chair of the 6G Alliance of Network AI, and the vice-chair of the THz Industry Alliance in China and the Wireless Technology Working Group of IMT-2030 (6G) Promotion Group supported by Ministry of Information and Industry Technology of China. He has been leading the 6G research and development with CMCC since 2018. He has led the Research and Development of 4G's evolution and 5G in CMCC from 2006 to 2020. He has acted as a Spectrum Working Group Chair and the Project Coordinator of LTE Evolution and 5G eMBB in the Global TD-LTE Initiative from 2013 to 2020 and led the industrialization and globalization of TD-LTE evolution and 5G eMBB.
YANG Yang is a professor with the IoT Thrust, the Director of the Research Center for the Digital World with Intelligent Things (DOIT), and the associate vice-president for Teaching and Learning with The Hong Kong University of Science and Technology (Guangzhou), China. He is also an adjunct professor with the Department of Broadband Communication at Peng Cheng Laboratory, the chief scientist of IoT with Terminus Group, and a senior consultant for Shenzhen Smart City Technology Development Group, China. His research interests include multi-tier computing networks, 5G/6G systems, AIoT technologies, intelligent services and applications, and advanced wireless testbeds. He has been the chair of the Steering Committee of the Asia-Pacific Conference on Communications (APCC) from 2019 to 2021. Currently, he is serving the IEEE Communications Society as the chair for the 5G Industry Community and chair for the Asia Region at Fog/Edge Industry Community. He is a fellow of IEEE.
ZHAO Zhifeng received his BE degree in computer science, ME degree in communication and information systems, and PhD degree in communication and information systems from the PLA University of Science and Technology, China in 1996, 1999, and 2002, respectively. From 2002 to 2004, he acted as a post-doctoral researcher with Zhejiang University, China, where his studies focused on multimedia next-generation networks (NGNs) and softswitch technology for energy efficiency. Currently, he is with the Zhejiang Lab as the Chief Engineering Officer. His research areas include software-defined networks (SDNs), wireless networks in 6G, computing networks, and collective intelligence. He is the Symposium Co-Chair of ChinaCom 2009 and 2010. He is the TPC Co-Chair of the 10th IEEE International Symposium on Communication and Information Technology (ISCIT 2010).
ZHANG Honggang is a professor with the Faculty of Data Science, City University of Macau, China. He was the founding Chief Managing Editor of Intelligent Computing, a Science Partner Journal, and a professor with the College of Information Science and Electronic Engineering, Zhejiang University, China. He was an Honorary Visiting Professor with the University of York, UK, and an International Chair Professor of Excellence with the Université Européenne de Bretagne and Supélec, France. His research interests include cognitive radio networks, semantic communications, green communications, machine learning, artificial intelligence, intelligent computing, and the Internet of Intelligence. He is a co-recipient of the 2021 IEEE Communications Society Outstanding Paper Award and the 2021 IEEE Internet of Things Journal Best Paper Award. He was the leading guest editor for the special issues on green communications of the IEEE Communications Magazine. He is the associate editor-in-chief of China Communications. He is a fellow of IEEE.
Supported by:
the National Key Research and Development Program of China(2024YFE0200600);the Zhejiang Provincial Natural Science Foundation of China(LR23F010005);the Huawei Cooperation Project(TC20240829036)

Abstract

Abstract:

Along with the proliferating research interest in semantic communication (SemCom), joint source channel coding (JSCC) has dominated the attention due to the widely assumed existence in efficiently delivering information semantics. Nevertheless, this paper challenges the conventional JSCC paradigm and advocates for adopting separate source channel coding (SSCC) to enjoy a more underlying degree of freedom for optimization. We demonstrate that SSCC, after leveraging the strengths of the Large Language Model (LLM) for source coding and Error Correction Code Transformer (ECCT) complemented for channel coding, offers superior performance over JSCC. Our proposed framework also effectively highlights the compatibility challenges between SemCom approaches and digital communication systems, particularly concerning the resource costs associated with the transmission of high-precision floating point numbers. Through comprehensive evaluations, we establish that assisted by LLM-based compression and ECCT-enhanced error correction, SSCC remains a viable and effective solution for modern communication systems. In other words, separate source channel coding is still what we need.

Key words: separate source channel coding (SSCC), joint source channel coding (JSCC), end-to-end communication system, Large Language Model (LLM), lossless text compression, Error Correction Code Transformer (ECCT)

REN Tianqi, LI Rongpeng, ZHAO Mingmin, CHEN Xianfu, LIU Guangyi, YANG Yang, ZHAO Zhifeng, ZHANG Honggang. Separate Source Channel Coding Is Still What You Need: An LLM-Based Rethinking[J]. ZTE Communications, 2025, 23(1): 30-44.

Figures/Tables 13

Table 1 Major notations used in this paper

Notation	Definition
$s, \hat{s}$	The transmitted text sequence and the recovered text sequenceat the receiver side
$t, \hat{t}$	The transmitted token sequence and the recovered token sequence at the receiver side
$C_{s}, C_{e}$	The source code and the channel code (error correction code)
$ρ, \tilde{ρ}$	The source distribution and the predicted probability distribution via LLM
$D, D_{i}, τ$	The dictionary of source coder, the i-th character in the dictionary, and the vocabulary of the dictionary
$I_{k}, l_{k}, u_{k}$	The probability interval in step k of source coding and its corresponding lower and upper bounds
$m, \hat{m}$	The message encoded by the source coder and the received (and channel decoded) message
$λ$	The probability interval, determined by the codeword, in a decimal form
$N, K$	The codeword length and message length of error correction code $C_{e} (N, K)$
$G, H$	The generator matrix and the parity check matrix
$x, x_{b}, x_{s}$	The transmitted codeword encoded by the channel coder and its binary and sign form
$\hat{x}, {\hat{x}}_{b}$	The soft approximation of codeword and its binary form
$N (\cdot, \cdot), σ_{n}$	The Gaussian distribution and the standard deviation of noise
$h$	The channel fading coefficient
$z, \tilde{z}, \hat{z}$	The additive Gaussian noise, as well as its corresponding multiplicative noise and the prediction result by ECCT
$y, y_{b}, \tilde{y}$	The noisy codeword, its binary form, and the result of pre-processing noisy codeword
$s y n (\cdot)$	The syndrome of codes defined in ECCT
$f (\cdot)$	The decoding function of ECCT
$W$	The learnable embedding matrix for high-dimensional mapping
$g (\cdot)$	The code-aware self-attention mask

Table 1 Major notations used in this paper

Notation	Definition
$s, \hat{s}$	The transmitted text sequence and the recovered text sequenceat the receiver side
$t, \hat{t}$	The transmitted token sequence and the recovered token sequence at the receiver side
$C_{s}, C_{e}$	The source code and the channel code (error correction code)
$ρ, \tilde{ρ}$	The source distribution and the predicted probability distribution via LLM
$D, D_{i}, τ$	The dictionary of source coder, the i-th character in the dictionary, and the vocabulary of the dictionary
$I_{k}, l_{k}, u_{k}$	The probability interval in step k of source coding and its corresponding lower and upper bounds
$m, \hat{m}$	The message encoded by the source coder and the received (and channel decoded) message
$λ$	The probability interval, determined by the codeword, in a decimal form
$N, K$	The codeword length and message length of error correction code $C_{e} (N, K)$
$G, H$	The generator matrix and the parity check matrix
$x, x_{b}, x_{s}$	The transmitted codeword encoded by the channel coder and its binary and sign form
$\hat{x}, {\hat{x}}_{b}$	The soft approximation of codeword and its binary form
$N (\cdot, \cdot), σ_{n}$	The Gaussian distribution and the standard deviation of noise
$h$	The channel fading coefficient
$z, \tilde{z}, \hat{z}$	The additive Gaussian noise, as well as its corresponding multiplicative noise and the prediction result by ECCT
$y, y_{b}, \tilde{y}$	The noisy codeword, its binary form, and the result of pre-processing noisy codeword
$s y n (\cdot)$	The syndrome of codes defined in ECCT
$f (\cdot)$	The decoding function of ECCT
$W$	The learnable embedding matrix for high-dimensional mapping
$g (\cdot)$	The code-aware self-attention mask

Figure 1 Framework of LLM-based and ECCT-complemented SSCC system

Figure 2 An example of arithmetic coding

Figure 3 LLM-based arithmetic encoding and decoding

Figure 4 ECCT architecture

Table 2 Mainly used hyperparameters in the experiments

Model	Hyperparameter	Value
ECCT	Learning rate	$10^{- 4}$
	Batch size	$128$
	Number of decoder layers	$6$
	Dimension of embedding	$32$
	Number of attention heads	$8$
DeepSC	Learning rate	$10^{- 4}$
	Batch size	$64$
	Number of encoder/decoder layers	$4$
	Dimension of embedding	$128$
	Dimension of FFN	$512$
	Number of attention heads	$8$
UT	Learning rate	$10^{- 4}$
	Batch size	$64$
	Number of encoder/decoder layers	$3$
	Dimension of embedding	$128$
	Dimension of FFN	$1 024$
	Number of attention heads	$8$

Table 2 Mainly used hyperparameters in the experiments

Model	Hyperparameter	Value
ECCT	Learning rate	$10^{- 4}$
	Batch size	$128$
	Number of decoder layers	$6$
	Dimension of embedding	$32$
	Number of attention heads	$8$
DeepSC	Learning rate	$10^{- 4}$
	Batch size	$64$
	Number of encoder/decoder layers	$4$
	Dimension of embedding	$128$
	Dimension of FFN	$512$
	Number of attention heads	$8$
UT	Learning rate	$10^{- 4}$
	Batch size	$64$
	Number of encoder/decoder layers	$3$
	Dimension of embedding	$128$
	Dimension of FFN	$1 024$
	Number of attention heads	$8$

Figure 5 BLEU and similarity scores versus SNRunified are evaluated for the same number of transmitted symbols. The proposed LLM-based SSCC is compared with Huffman coding with LDPC49,?24 in BPSK, DeepSC, UT, and UT with quantization under the AWGN channel

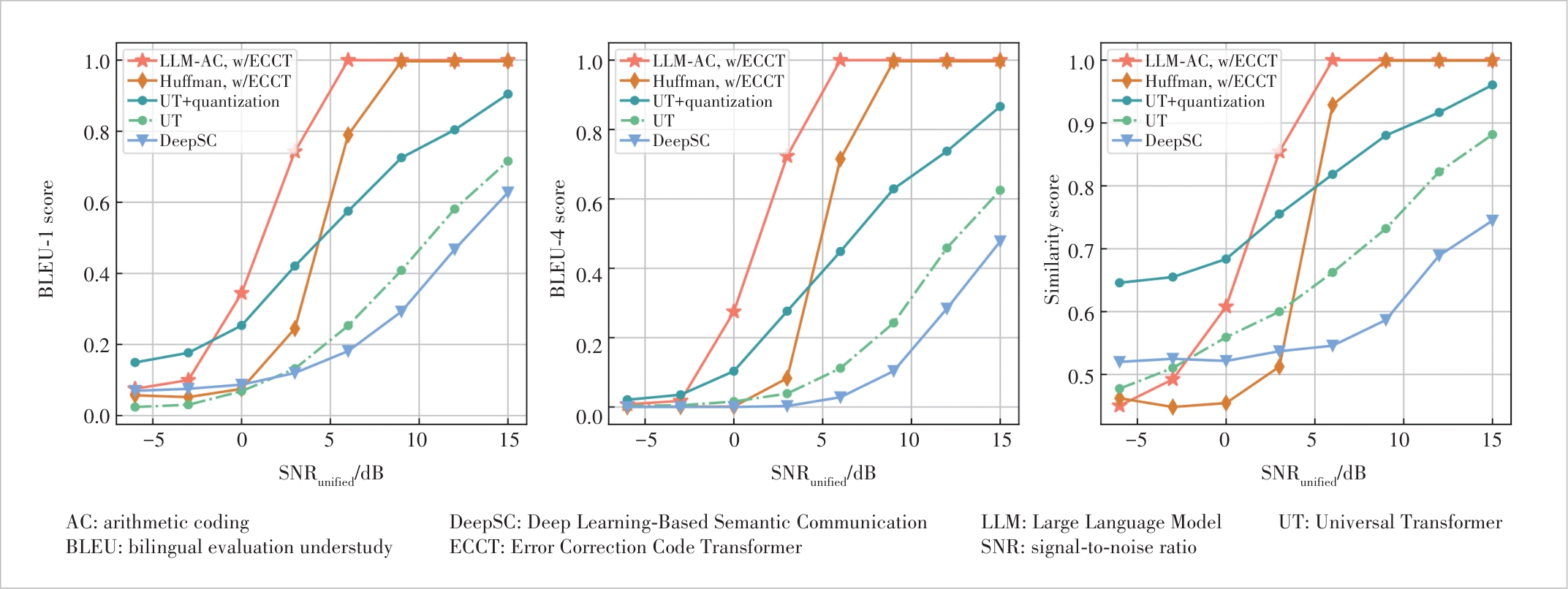
Figure 6 BLEU and similarity scores versus SNRunified are evaluated for the same number of transmitted symbols. The proposed LLM-based SSCC is compared with Huffman coding with LDPC49,?24 in BPSK; DeepSC, UT, and UT with quantization trained under the Rayleigh fading channel

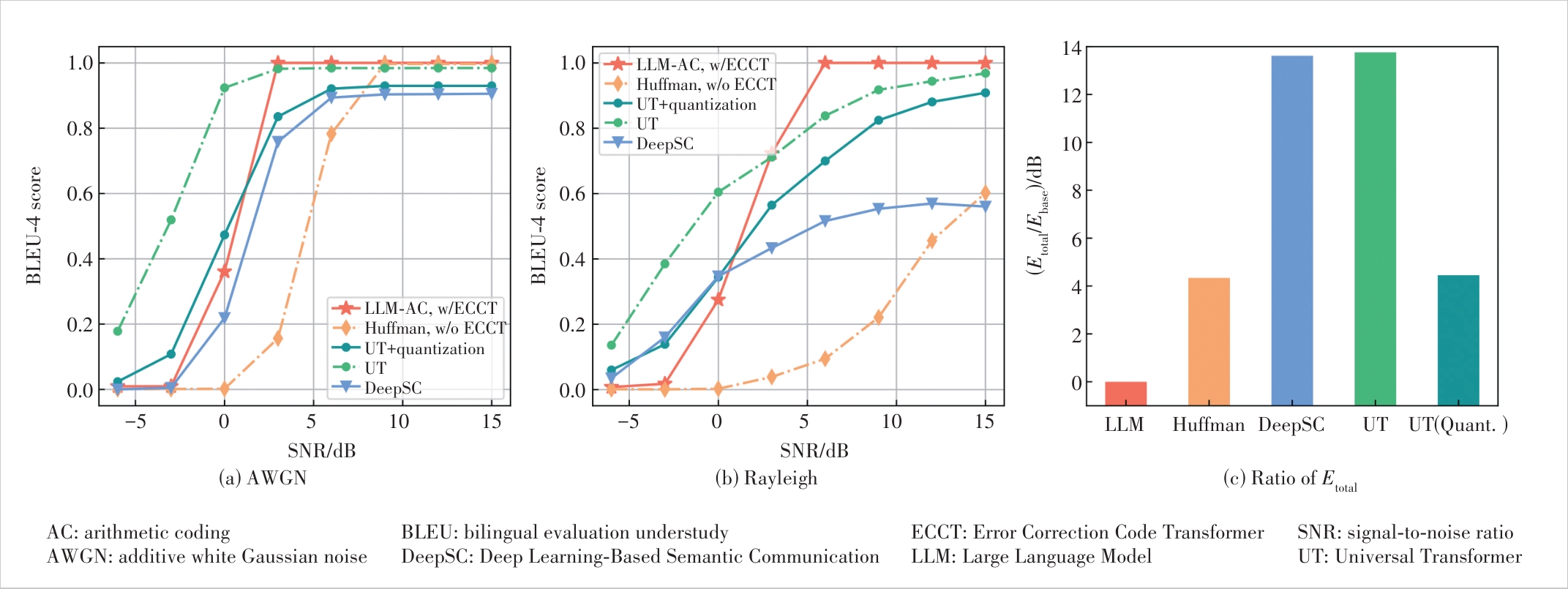
Figure 7 BLEU-4 score versus SNR is evaluated for the same number of transmitted symbols. The proposed LLM-based SSCC is compared with Huffman coding with LDPC49,?24 in BPSK (without ECCT), DeepSC, UT, and UT with quantization trained under (a) AWGN and (b) Rayleigh fading channels; (c) shows the ratio of Etotal among different systems

Figure 8 BLEU-4 score versus SNRunified for the same number of transmitted symbols, with different code rates using LDPC49,?24?/LDPC49,?30/LDPC49,?36 in BPSK, compared with the situations removing ECCT, under (a) AWGN and (b) Rayleigh fading channels

Figure 9 BLEU and similarity scores of models versus SNRunified, with different parameter scales (GPT2, GPT2-medium, GPT2-large, GPT2-XL), using LDPC121,?110 as the error correction code

Figure 10 Compression rate comparison between traditional methods (Zlib and Huffman coding) and LLM-AC

Table 3 Influence of token block sizes on system performance during LLM-based arithmetic source encoding for SNR={-6, 0, 6}

Block size	Similarity			BLEU-1			BLEU-4
Block size	-6	0	6	-6	0	6	-6	0	6
16	$0.770 8$	$0.915 7$	$0.999 3$	$0.197 5$	$0.645 2$	$0.987 7$	$0.007 2$	$0.508 1$	$0.983 0$
32	$0.712 3$	$0.935 9$	$0.998 4$	$0.172 5$	$0.584 2$	$0.978 7$	$0.005 5$	$0.466 6$	$0.969 4$
64	$0.700 1$	$0.893 8$	$0.999 9$	$0.116 0$	$0.580 1$	$0.996 9$	$0.001 8$	$0.427 0$	$0.992 2$
128	$0.758 7$	$0.857 3$	$0.999 9$	$0.183 1$	$0.434 4$	$0.999 9$	$0.003 8$	$0.252 9$	$0.999 9$

Table 3 Influence of token block sizes on system performance during LLM-based arithmetic source encoding for SNR={-6, 0, 6}

Block size	Similarity			BLEU-1			BLEU-4
Block size	-6	0	6	-6	0	6	-6	0	6
16	$0.770 8$	$0.915 7$	$0.999 3$	$0.197 5$	$0.645 2$	$0.987 7$	$0.007 2$	$0.508 1$	$0.983 0$
32	$0.712 3$	$0.935 9$	$0.998 4$	$0.172 5$	$0.584 2$	$0.978 7$	$0.005 5$	$0.466 6$	$0.969 4$
64	$0.700 1$	$0.893 8$	$0.999 9$	$0.116 0$	$0.580 1$	$0.996 9$	$0.001 8$	$0.427 0$	$0.992 2$
128	$0.758 7$	$0.857 3$	$0.999 9$	$0.183 1$	$0.434 4$	$0.999 9$	$0.003 8$	$0.252 9$	$0.999 9$

References 58

1	LU Z L, LI R P, LU K. Semantics-empowered communication: a tutorial-cum-survey [J]. IEEE communications surveys and tutorials, 2024, 26(1): 41–79. DOI: 10.1109/COMST.2023.333334
2	KURKA D B, GÜNDÜZ D. DeepJSCC-f: deep joint source-channel coding of images with feedback [J]. IEEE journal on selected areas in information theory, 2020, 1(1): 178–193. DOI: 10.1109/JSAIT.2020.2987203
3	BAO Z C, LIANG H T, DONG C, et al. MDVSC: wireless model division video semantic communication for 6G [C]//Proc. IEEE Globecom Workshops (GC Wkshps). IEEE, 2023: 1572–1578. DOI: 10.1109/GCWkshps58843.2023.10464666
4	JIA Y J, HUANG Z, LUO K, et al. Lightweight joint source-channel coding for semantic communications [J]. IEEE communications letters, 2023, 27(12): 3161–3165. DOI: 10.1109/LCOMM.2023.3329533
5	LIU S C, GAO Z, CHEN G J, et al. Transformer-based joint source channel coding for textual semantic communication [C]//Proc. IEEE/CIC International Conference on Communications in China (ICCC). IEEE, 2023: 1–6. DOI: 10.1109/ICCC57788.2023.10233424
6	LIU X Y, HUANG Z, ZHANG Y L, et al. CNN and attention-based joint source channel coding for semantic communications in WSNs [J]. Sensors, 2024, 24(3): 957. DOI: 10.3390/s24030957
7	LU Z L, LI R P, LEI M, et al. Self-critical alternate learning based semantic broadcast communication [J]. IEEE transactions on communications, 2024: 1. DOI: 10.1109/tcomm.2024.3487513
8	TONG W J, LIU F F, SUN Z F, et al. Image semantic communications: an extended rate-distortion theory based scheme [C]//Proc. IEEE Globecom Workshops (GC Wkshps). IEEE, 2022: 1723–1728. DOI: 10.1109/GCWkshps56602.2022.10008733
9	TONG S Y, YU X X, LI R P, et al. Alternate learning based sparse semantic communications for visual transmission [C]//Proc. 34th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC). IEEE, 2023. DOI: 10.1109/pimrc56721.2023.10293971
10	TONG S Y, YU X X, LI R P, et al. Alternate learning-based SNR-adaptive sparse semantic visual transmission [J]. IEEE transactions on wireless communications, 2025, 24: 1737–1752. DOI: 10.1109/TWC.2024.3512652
11	WANG J, WANG S X, DAI J C, et al. Perceptual learned source-channel coding for high-fidelity image semantic transmission [C]//Proc. IEEE Global Communications Conference. IEEE, 2022: 3959–3964. DOI: 10.1109/GLOBECOM48099.2022.10001359
12	XIE H Q, QIN Z J, LI G Y, et al. Deep learning enabled semantic communication systems [J]. IEEE transactions on signal processing, 2021, 69: 2663–2675. DOI: 10.1109/tsp.2021.3071210
13	ZHANG W Y, BAI K Y, ZEADALLY S, et al. DeepMA: end-to-end deep multiple access for wireless image transmission in semantic communication [J]. IEEE transactions on cognitive communications and networking, 10(2): 387–402. DOI: 10.1109/tccn.2023.3326302
14	ZHOU Q Y, LI R P, ZHAO Z F, et al. Semantic communication with adaptive universal transformer [J]. IEEE wireless communications letters, 2022, 11(3): 453–457. DOI: 10.1109/LWC.2021.3132067
15	GOYAL M, TATWAWADI K, CHANDAK S, et al. DeepZip: lossless data compression using recurrent neural networks [C]//Proc. Data Compression Conference (DCC). IEEE, 2019. DOI: 10.1109/dcc.2019.00087
16	BELLARD F. Lossless data compression with neural networks [EB/OL]. (2019-05-04)[2024-11-20].
17	LIU Q, XU Y L, LI Z. DecMac: a deep context model for high efficiency arithmetic coding [C]//Proc. International Conference on Artificial Intelligence in Information and Communication (ICAIIC). IEEE, 2019. DOI: 10.1109/icaiic.2019.8668843
18	GOYAL M, TATWAWADI K, CHANDAK S, et al. DZip: improved general-purpose loss less compression based on novel neural network modeling [C]//Proc. Data Compression Conference (DCC). IEEE, 2021. DOI: 10.1109/dcc50243.2021.00023
19	VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need [C]//Proc. 31st International Conference on Neural Information Processing Systems. NIPS, 2017: 6000–6010
20	HUANG C, XIE Y Q, JIANG Z Y, et al. Approximating human-like few-shot learning with GPT-based compression [EB/OL]. (2023-08-14)[2024-11-12].
21	MITTU F, BU Y H, GUPTA A, et al. FineZip: pushing the limits of large language models for practical lossless text compression [EB/OL]. (2024-09-25)[2024-11-12].
22	MAO Y, CUI Y F, KUO T W, et al. A fast transformer-based general-purpose lossless compressor [EB/OL]. (2022-03-30)[2024-11-12].
23	NARASHIMAN S S, CHANDRACHOODAN N. AlphaZip: neural network-enhanced lossless text compression [EB/OL]. (2024-09-23)[2024-11-12].
24	VALMEEKAM C S K, NARAYANAN K, KALATHIL D, et al. LLMZip: Lossless text compression using large language models [EB/OL]. (2023-06-06)[2024-11-12]
25	DELÉTANG G, RUOSS A, P-A DUQUENNE, et al. Language modeling is compression [EB/OL]. (2023-09-19)[2024-10-20].
26	BOSE R C, RAY-CHAUDHURI D K. On a class of error correcting binary group codes [J]. Information and control, 1960, 3(1): 68–79. DOI: 10.1016/s0019-9958(60)90287-4
27	GALLAGER R. Low-density parity-check codes [J]. IRE transactions on information theory, 1962, 8(1): 21–28. DOI: 10.1109/TIT.1962.1057683
28	ARIKAN E. Channel polarization: a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels [J]. IEEE transactions on information theory, 2009, 55(7): 3051–3073. DOI: 10.1109/TIT.2009.2021379
29	NACHMANI E, BE'ERY Y, BURSHTEIN D. Learning to decode linear codes using deep learning [C]//Proc. 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton). IEEE, 2016: 341–346. DOI: 10.1109/ALLERTON.2016.7852251
30	NACHMANI E, MARCIANO E, LUGOSCH L, et al. Deep learning methods for improved decoding of linear codes [J]. IEEE journal of selected topics in signal processing, 12(1): 119–131. DOI: 10.1109/jstsp.2017.2788405
31	NACHMANI E, WOLF L. Hyper-graph-network decoders for block codes [C]//Proc. 33st International Conference on Neural Information Processing Systems. NIPS, 2019: 2329–2339
32	CHOUKROUN Y, WOLF L. Error correction code transformer [C]//Proc. 36st International Conference on Neural Information Processing Systems. NIPS, 2022: 38695–38705
33	HUANG J H, YUAN K, HUANG C, et al. D2 -JSCC: digital deep joint source-channel coding for semantic communications [EB/OL]. (2024-03-12)[2024-11-20].
34	JIANG P W, WEN C K, YI X P, et al. Semantic communications using foundation models: design approaches and open issues [J]. IEEE wireless communications, 2024, 31(3): 76–84. DOI: 10.1109/MWC.002.2300460
35	LIANG C S, DU H Y, SUN Y, et al. Generative AI-driven semantic communication networks: architecture, technologies and applications [J]. IEEE transaction on cognitive communications and networking, 2024, early access. DOI: 10.1109/TCCN.2024.3435524
36	JIANG F B, PENG Y B, DONG L, et al. Large AI model-based semantic communications [J]. IEEE wireless communications, 31(3): 68–75. DOI: 10.1109/mwc.001.2300346
37	GRASSUCCI E, BARBAROSSA S, COMMINIELLO D. Generative semantic communication: diffusion models beyond bit recovery [EB/OL]. (2023-06-07)[2024-11-12].
38	CHANG M K, HSU C T, YANG G C. GenSC: generative semantic communication systems using BART-like model [J]. IEEE communications letters, 2024, 28(10): 2298–2302. DOI: 10.1109/LCOMM.2024.3450309
39	GUO S S, WANG Y H, LI S J, et al. Semantic importance-aware communications using pre-trained language models [J]. IEEE communications letters, 2023, 27(9): 2328–2332. DOI: 10.1109/LCOMM.2023.3293805
40	XIE H Q, QIN Z J, TAO X M, et al. Toward intelligent communications: large model empowered semantic communications [J]. IEEE communications magazine, 2025, 63(1): 69–75. DOI: 10.1109/MCOM.001.2300807
41	QIAO L, MASHHADI M B, GAO Z, et al. Latency-aware generative semantic communications with pre-trained diffusion models [EB/OL]. (2024-03-05)[2024-11-12].
42	JIANG F B, DONG L, PENG Y B, et al. Large AI model empowered multimodal semantic communications [J]. IEEE communications magazine, 2025, 63(1): 76–82. DOI: 10.1109/mcom.001.2300575
43	YANG W T, XIONG Z H, MAO S W, et al. Rethinking generative semantic communication for multi-user systems with large language models [EB/OL]. (2024-08-16)[2024-11-12].
44	SHANNON C E. A mathematical theory of communication [J]. Bell system technical journal, 1948, 27(3): 379–423. DOI: 10.1002/j.1538-7305.1948.tb01338.x
45	RISSANEN J J. Generalized kraft inequality and arithmetic coding [J]. IBM journal of research and development, 1976, 20(3): 198–203. DOI: 10.1147/rd.203.0198
46	PASCO R. Source coding algorithms for fast data compression (Ph.D. Thesis abstr.) [J]. IEEE transactions on information theory, 1977, 23(4): 548. DOI: 10.1109/TIT.1977.1055739
47	HOWARD P G, VITTER J S. Arithmetic coding for data compression [J]. Proceedings of the IEEE, 1994, 82(6): 857–865. DOI: 10.1109/5.286189
48	BENNATAN A, CHOUKROUN Y, KISILEV P. Deep learning for decoding of linear codes: a syndrome-based approach [C]//Proc. IEEE International Symposium on Information Theory (ISIT). IEEE, 2018: 1595–1599. DOI: 10.1109/ISIT.2018.8437530
49	KOEHN P. Europarl: a parallel corpus for statistical machine translation [C]//Proc. Machine Translation Summit. International Association for Machine Translation, 2005: 79–86
50	RADFORD A, WU J, CHILD R, et al. Language models are unsupervised multitask learners [EB/OL]. [2024-10-20].
51	PAPINENI K, ROUKOS S, WARD T, et al. BLEU: a method for automatic evaluation of machine translation [C]//Proc. 40th Annual Meeting on Association for Computational Linguistics. USAACL, 2001. DOI: 10.3115/1073083.1073135
52	DEVLIN J, CHANG M-W, LEE K, et al. BERT: pre-training of deep bidirectional transformers for language understanding [C]//Proc. 2019 Conference of the North American Chapter of the Association for Computational Linguistics (NAACL), Association for Computational Linguistics, 2019: 4171–4186. DOI: 10.18653/v1/N19-1423
53	CHOUKROUN Y, WOLF L. Denoising diffusion error correction codes [EB/OL]. (2022-09-16)[2024-11-12].
54	HUANG Y Z, ZHANG J H, SHAN Z F, et al. Compression represents intelligence linearly [EB/OL]. (2024-04-15)[2024-11-12].
55	PARK S J, KWAK H Y, KIM S H, et al. How to mask in error correction code transformer: systematic and double masking [EB/OL]. (2023-08-16)[2024-11-12].
56	NGUYEN D T, KIM S. U-shaped error correction code transformers [J]. IEEE transactions on cognitive communications and networking, 2024: 1. DOI: 10.1109/tccn.2024.3482349
57	HO J, JAIN A, ABBEEL P. Denoising diffusion probabilistic models [C]//Proc. 34th International Conference on Neural Information Processing Systems. NIPS, 2020: 6840–6851. DOI: 10.48550/arXiv.2006.11239
58	CHOUKROUN Y, WOLF L. A foundation model for error correction codes [C]//12th International Conference on Learning Representations. ICLR, 2024. DOI: 10.48550/arXiv.2405.04050

Separate Source Channel Coding Is Still What You Need: An LLM-Based Rethinking

RichHTML

PDF

Knowledge

Abstract

Cite this article

share this article

Figures/Tables 13

References 58

Related Articles 0

Recommended Articles 0

Metrics